Background

Motivation

Since the beginning of my PhD, I’ve been interested in a quantitative understanding of intelligence, both artificial and biological — and in the possible relationship between the two. I am mainly focused on neural network models, which are a canonical model for neural computation in the brain and are a central part of many modern artificial intelligence systems.

Such artificial neural networks with deep architectures have dramatically improved the state-of-the-art in computer vision, speech recognition, natural language processing, and many other domains.

Despite this impressive progress, artificial neural networks are still far behind the capabilities of biological neural networks in most areas: even the simplest fly is far more resourceful than our most advanced robots. This indicates we have much to improve!

At the same time, if we wish to understand biological neural networks we must first be able to understand learning in the simplest non-linear artificial neural network – which still remains a mystery.

Over the years my research aimed to uncover the fundamental mathematical principles governing both types of neural networks. Since I started my faculty position in the Technion, I focused on artificial neural networks, in the context of machine learning.

Past and current research interests

My research so far covered many aspects of neural networks and deep learning. See below more information on a few open questions that interested me during my academic life.

Current research: Deep Learning

• Learning and optimization in artificial neural networks
• Resource efficient training and inference in artificial neural networks
• Hardware implementations of artificial neural networks

Post-Doc research: Neuroscience Methods

• Activity inference
• Model based connectivity
• Efficient simulation methods

PhD research: Neuroscience Theory

Modeling and analysis of

• Biological neural networks
• Neurons
• Synapses
• Ion channels

My Current Research: Deep Learning

There are several open theoretical questions in deep learning. Answering these theoretical questions will provide design guidelines and help with some important practicals issue (explained below). Two central questions are:

• Low training error. Neural Networks are often initialized randomly, and then optimized using local steps with stochastic gradient descent (SGD). Surprisingly, we often observe that SGD converges to a low training error:

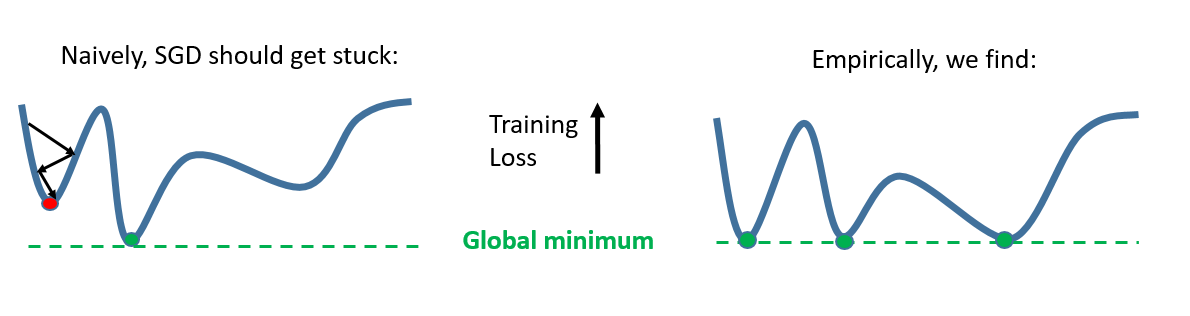
Why is it happening?

• Low generalization error. Neural Networks are ofter trained in a regime where #parameters » #data samples. Surprisingly, these networks generalize well in such a regime, even when there is no explicit regularization.

For example, as can be seen in the figure below from Wu, Zu & E 2017 , polyomial curves (right) tend to overfit much more than neural networks (left):

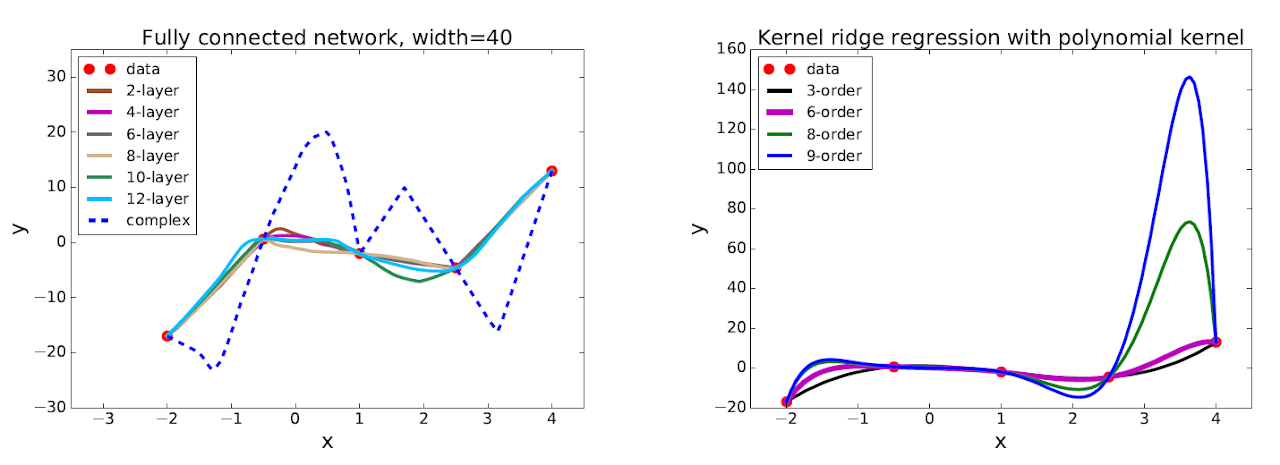
Why is it happening?

There are many practical bottlenecks in deep learining (the following fifures are from Sun et al. 2017.Such bottlenecks occur since neural networks models are large, and keep getting larger over the years:

• Computational resources. Using larger neural networks require more computational resources, such as power-hungry GPUs:

How can we train and use neural networks more efficiently (i.e., better speed, energy, memory), without sacrificing accuracy? See my talk here (in Hebrew) for some of our results on this.

• Labeled data. In order to train neural nets to high accuracy levels, large quantities of labeled data are required. Such datasets are hard to obtain. For example, for many years the size of the largest vision training data remained constant:

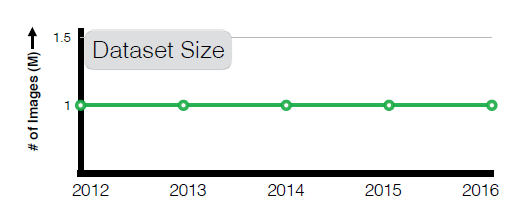
How can we decrease the amount of label data required for training?

• Choosing hyper-parameters. Since larger models take longer to train, it becomes more challenging to choose model hyper-parameters (e.g., architecture, learning rate) in order to obtain good performance.

For example, ad can be seen in this (video) Xiang&Li 2017 , small changes in the training procedure have a large effect on the network performance.

Can we find automatic and robust method to find the “optimal” hyper-parameters?

My Post-doc Research: Neuroscience Methods

Neuroscience datasets are typically very challenging. They are usually very noise, of limited duration, and are affected by many unobserved latent variables. Analyzing and modeling these datasets becomes more and more challenging over the years, since the number of recorded neurons increases exponentially, similarly to “Moore’s law” (Figure from Stevenson&Kording 2011):

In order to analyze neuroscience data, certain inference tasks are typically necessary to be able to interpret the data:

• Activity inference. Neural activity is often measured optically: each neuron is edited genetically so it emits fluorescent pulses whenever it fires a “spike”. For example (from Aherns et al. 2013) see this video

Can we infer the “spiking” firing patterns of each neuron from the observed movie? This includes automatic localization of each neurons, demixing of signals from nearby neurons, denoising and deconvlusion of the observed fluorescence to obtain the original “spikes”.

• Connectivity estimation.Given the activity patterns of various neurons in the network, can we infer their synaptic and functional connectivity?

• Efficient simulation.Accurately simulating large network models, or even highly detailed single neuron models can be very slow and inefficient. Can we improve the simulation methods?

My PhD research: Neuroscience Theory

A central issue in neuroscience is to find the “appropriate” level of modeling: in every level and component of the nervous system we find complex biophysical machinery that affects their functional input output relation. There are many possible levels of modeling:

• Network model. Given some observed phenomenon, such as the formation of hexgonal grid cells see this video

What is the simplest neural network model that reproduces this phenomenon, and produces useful (disprovable) predictions? Can we infer from this model the “purpose” of this neural circuit?

• Neuron model. Even a single neuron in synaptic isolation, given direct periodic pulse stimulation, can produce very complicated firing patterns over the timescales of days (Figure from Gal et al. 2010, a vector of response/no-response folded to matrix over 55 hours):

Given such biophysical and functional complexity, how can we build and analyze useful neural models, with meaningful predictions?

• Neuronal components. Even sub-cellular components such as a synapses, or an ion channel are incredibly complex and can respond stochasticly to stimuli on very long and multiple timescales. For example, here are synaptic strength seems to evolve stochasticaly over timescales weeks (Minerbi et al. 2009). See this video.

How can memory of past events be retained in the brain despite these large changes? Can we find the simplest “effective” input-output relation that can be used to model single neurons?