Research: Algorithmic Bias Control in Deep learning
(A-B-C-Deep, an ERC Project)
Deep Learning (DL) has reached unparalleled performance in many domains. However, this impressive performance typically comes at the cost of gathering large datasets and training massive models, requiring extended time and prohibitive costs. Significant research efforts are being invested in improving DL training efficiency, i.e., the amount of time, data, and resources required to train these models, by changing the model (e.g., architecture, numerical precision) or the training algorithm (e.g., parallelization). Other modifications aim to address critical issues, such as credibility and over-confidence, which hinder the implementation of DL in the real world. However, such modifications often cause an unexplained degradation in the generalization performance of DL to unseen data. Recent findings suggest that this degradation is caused by changes to the hidden algorithmic bias of the training algorithm and model. This bias selects a specific solution from all solutions which fit the data. After years of trial-and-error, this bias in DL is often at a “sweet spot” which implicitly allows ANNs to learn well, due to unknown key design choices. But performance typically degrades when these choices change. Therefore, understanding and controlling algorithmic bias is the key to unlocking the true potential of deep learning.
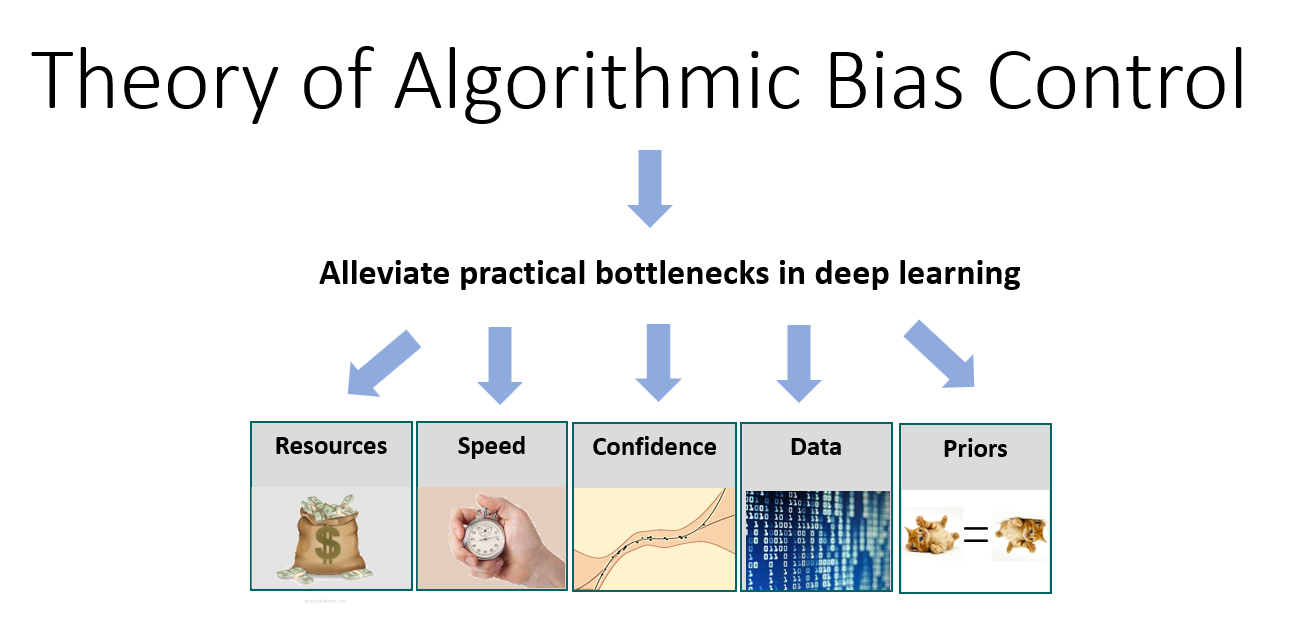
Our goal is to develop a rigorous theory of algorithmic bias in DL and to apply it to alleviate critical practical bottlenecks that prevent such models from scaling up or implemented in real-world applications.
Our approach has three objectives: (1) identify the algorithmic biases affecting DL; (2) understand how these biases affect the functional capabilities and generalization performance; and (3) control these biases to alleviate critical practical bottlenecks. To demonstrate the feasibility of this challenging project, we describe how recent advances and concrete preliminary results enable us to effectively approach all these objectives.
All research published in the frame of this project:
The sign * indicates equal contribution of the authors.
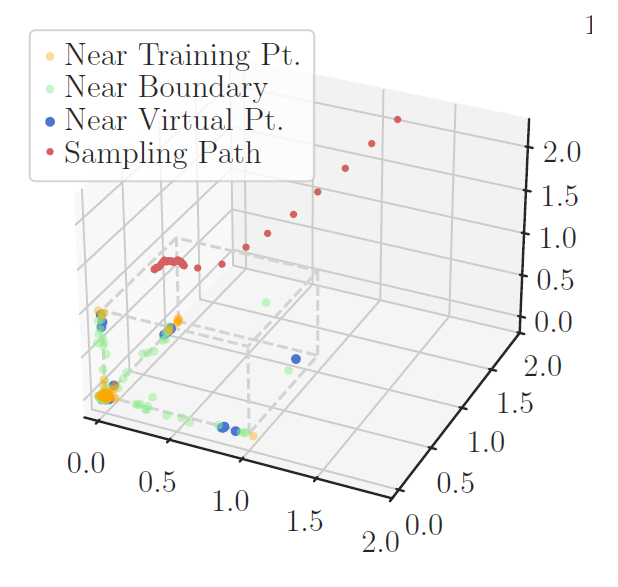
We analytically solve score- and probability-flows for certain datasets, and show the implications for training data memorization.
C. Zeno, H. Manor, G. Ongie, N. Weinberger, T. Michaeli, D. Soudry
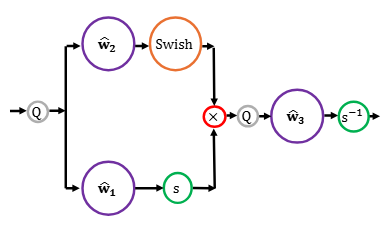
We show how train to LLMs in FP8, even when trained at the scale of trillions of tokens. We analytically and empirically pinpoint the problem in the SwiGLU activation and propose a solution.
M. Fishman, B. Chmiel, R. Banner, D. Soudry
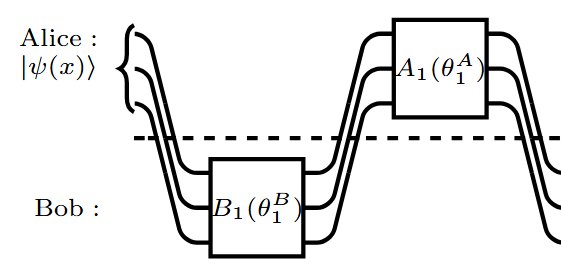
We show the first example of exponential quantum advantage for a generic class of machine learning problems that hold regardless of the data encoding cost.
H. Michaeli, D. Gilboa, D. Soudry, J. R. McClean
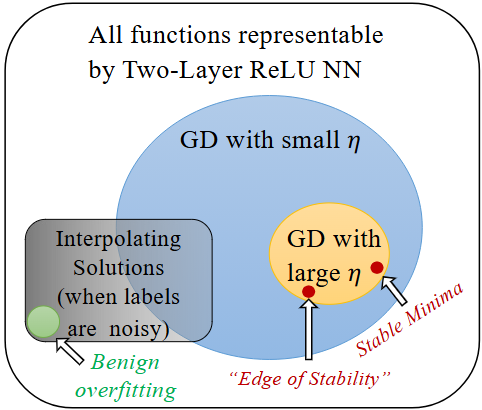
We are the first to obtain generalization bound via minima stability in the non-interpolation case and the first to show ReLU NNs without regularization can achieve near-optimal rates in nonparametric regression.
D. Qiao, K. Zhang, E. Singh, D. Soudry, and Y. X. Wang
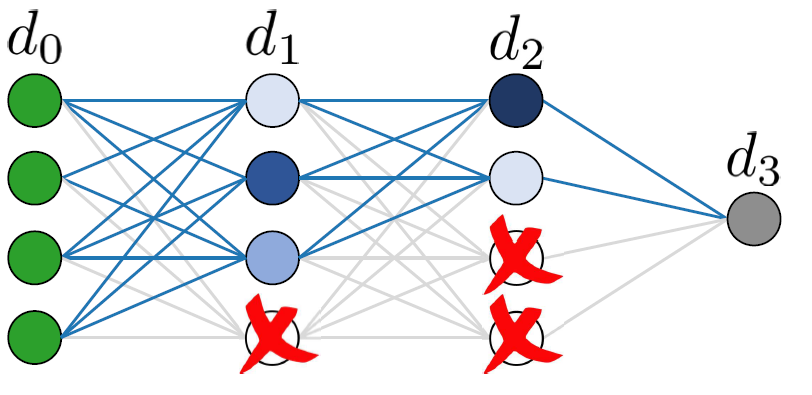
We prove (empirically observed) tempered overfitting happens in quantized deep neural nets found using the minimal sizeed interpolate or a random interpolator
I. Harel, W. M. Hoza, G. Vardi, I, Evron, N. Srebro, D. Soudry
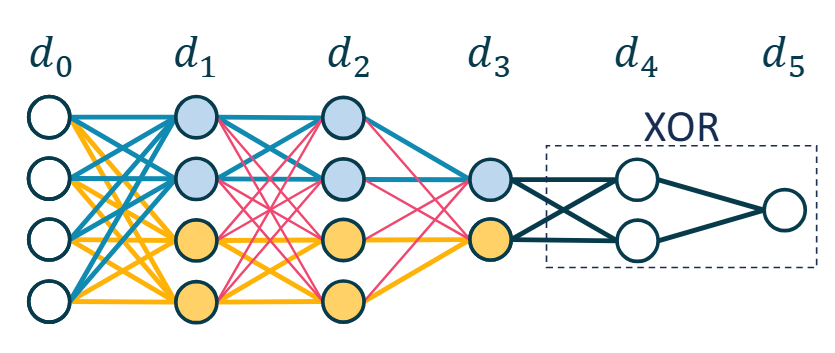
We prove the max-margin results on various classifcation losses with linear predictors on separable multiclass data
H. Ravi, C. Scott, D. Soudry, Y. Wang
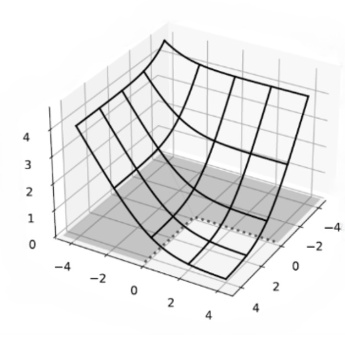
We examine neural networks (NN) with uniform random weights, conditioned on zero training loss. We prove they typically generalize well if there exists an underlying narrow ``teacher NN” that agrees with the labels.
G. Buzaglo *, I. Harel *, M. Shpigel Nacson *, A. Brutzkus, N. Srebro, D. Soudry
ICML 2024 (Spotlight, 3.5% acceptance rate)

We present a simple method to enable, for the first time, the usage of 12-bits accumulators in deep learning, with no significant degradation in accuracy. Also, we show that as we decrease the accumulation precision further, using fine-grained gradient approximations can improve the DNN accuracy.
Y. Blumenfeld, I. Hubara, D. Soudry
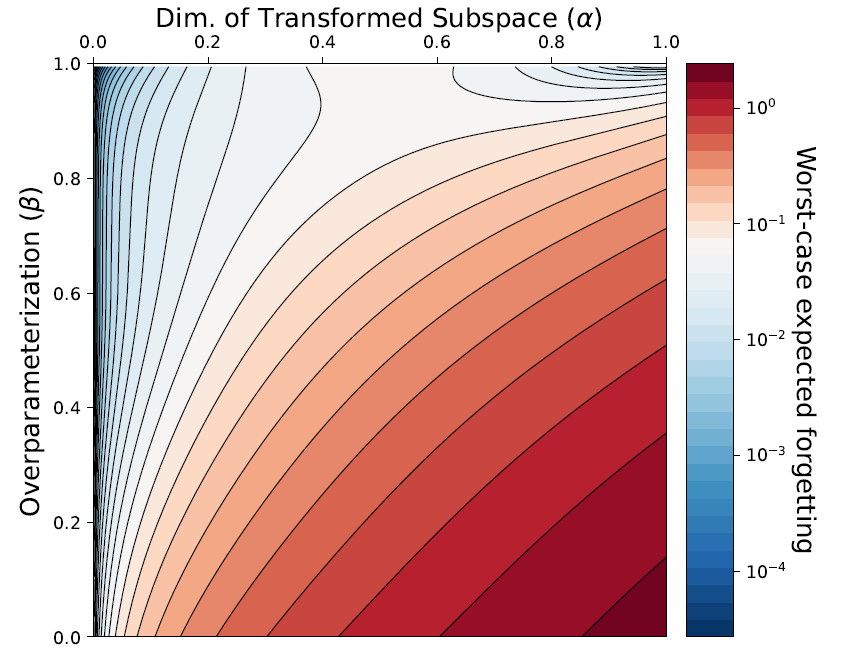
We examine how task similarity and overparameterization jointly affect forgetting in an analyzable model.
D. Goldfarb *, I. Evron *, N. Weinberger, D. Soudry, P. Hand
In this paper, we aim to characterize the functions realized by shallow ReLU NN denoisers – in the common theoretical setting of interpolation (i.e., zero training loss) with a minimal representation cost.
C. Zeno, G. Ongie, Y. Blumenfeld, N. Weinberger, D. Soudry
We find an analytical relation between compute time properties and scalability limitations, caused by the compute variance of straggling workers in a distributed setting. Then, we propose a simple yet effective decentralized method to reduce the variation among workers and thus improve the robustness of synchronous training.
N. Giladi *, S. Gottlieb * , M. Shkolnik, A. Karnieli, R. Banner, E. Hoffer, K. Y. Levy, D. Soudry
We study zero-shot generalization in reinforcement learning—optimizing a policy on a set of training tasks to perform well on a similar but unseen test task.
E. Zisselman, I. Lavie, D. Soudry, A. Tamar
We find a quantity that does decrease monotonically throughout GD training - the sharpness attained by the gradient flow solution (GFS).
I Kreisler * , M. Shpigel Nacson * ,D. Soudry, Y. Carmon
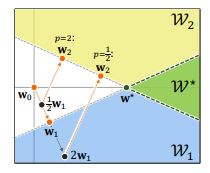
We analyze continual learning on a sequence of separable linear classification tasks with binary labels. We show theoretically that learning with weak regularization reduces to solving a sequential max-margin problem, corresponding to a special case of the Projection Onto Convex Sets (POCS) framework.
I. Evron, E. Moroshko, G. Buzaglo, M. Khriesh, B. Marjieh, N. Srebro, D. Soudry
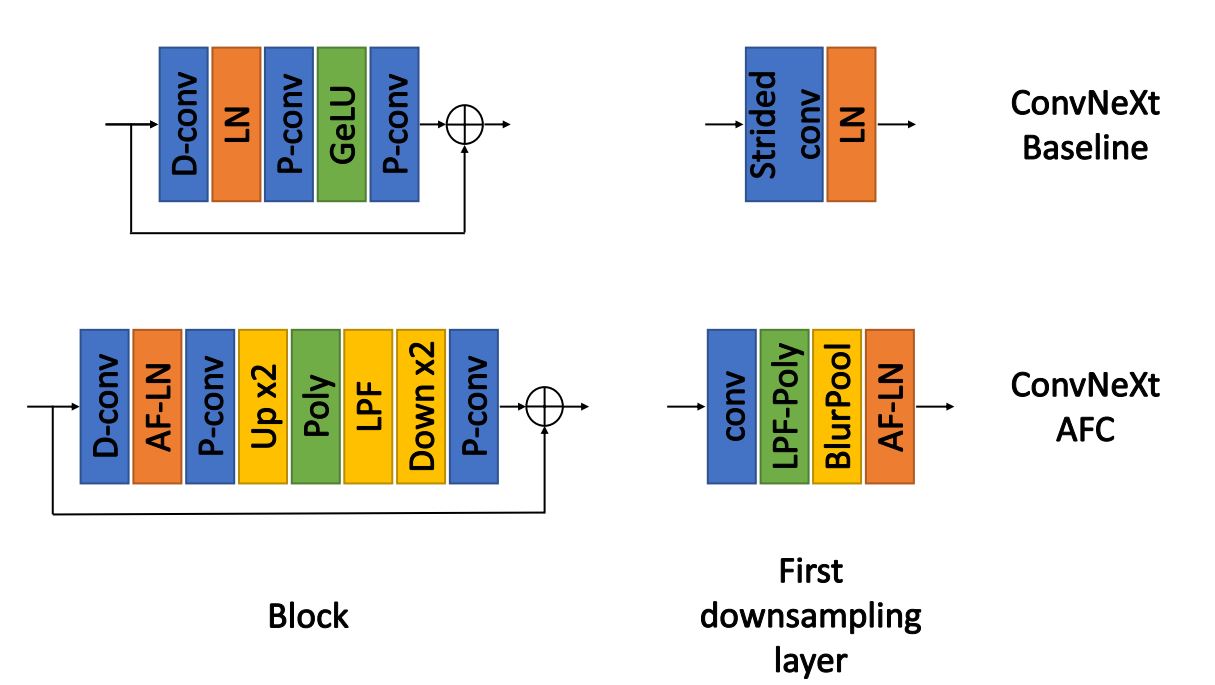
We propose an extended anti-aliasing method that tackles both downsampling and non-linear layers, thus creating truly alias-free, shift-invariant CNNs.
H. Michaeli, T. Michaeli, D. Soudry
See more details about this paper
We study the type of solutions to which stochastic gradient descent converges when used to train a single hidden-layer multivariate ReLU network with the quadratic loss. Our results are based on a dynamical stability analysis.
M. Shpigel Nacson, R. Mulayoff, G. Ongie, T. Michaeli, D. Soudry
Previous works separately showed that accurate 4-bit quantization of the neural gradients needs to (1) be unbiased and (2) have a log scale. However, no previous work aimed to combine both ideas, as we do in this work. Specifically, we examine the importance of having unbiased quantization in quantized neural network training, where to maintain it, and how to combine it with logarithmic.
B. Chmiel, R. Banner, E. Hoffer, H. Ben Yaacov, D. Soudry
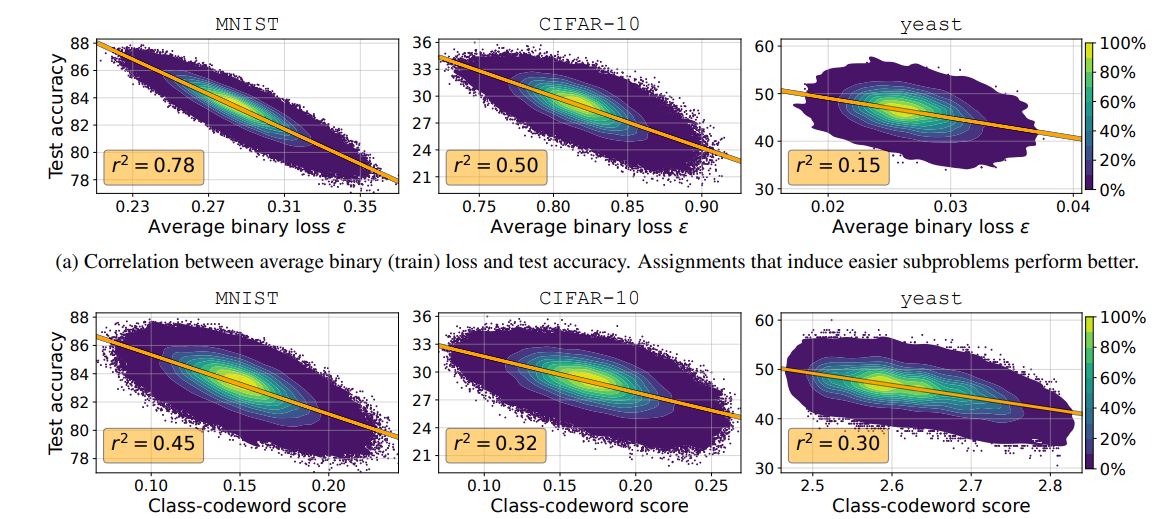
Our paper shows that these assignments play a major role in the performance of ECC. Specifically, we examine similarity-preserving assignments, where similar codewords are assigned to similar classes.
I. Evron * , O. Onn * , T. Weiss, H. Azeroual, D. Soudry
This project has received funding from the European Union’s Horizon Europe research and innovation programme under grant agreement No 101039436-ERC-A-B-C-Deep.